を単連結領域上の正則関数とするとき，任意の区分的になめらかな閉曲線に たいして，

　このTh．に学部生の頃なぜか惹かれた．何かとても不思議な感じがするのだった．表現もとてもsimpleで，他の複素関数のlevelの高いelegantな表現にelegantさを
感じられない自分としては，少なくともこれくらいはと思ったものである．

遡って高校時代に、次のような問題があった．

方程式の３根をとし，方程式が2根をもつとする．このとき，Gauss平面で　を表す点がで表される点で作られる三角形の内部または線分上にあることを証明せよ．但しはすべて異なるとする．

　この問題がなかなか解けなくて，ついに次のような解答を考えた．直接授業では教えていただかなったが，問題解法のtechnicianとして知られるＳ先生に相談したところ，微分するのはまずいのではないかとのことだった．Ｓ先生はいつも問題を一目見ると，いきなり解答を説明するのが常だった．このときもすぐに説明を始めてしばらくすると，・・・・・

その後１時間位数研で説明というか先生が悩んでいたのを見ていた．その後どうなったかは記憶に残っていない．

解答

３点で作られる三角形の内部又は線分上の点は一般に

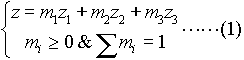
で表されるから，　が(1)で表されるこ示す．

題意より次のようにおける．

よって

(2)，(3)より　　

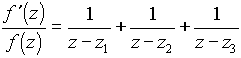
ここで，方程式

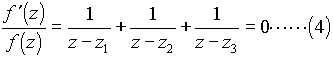
を考えると，(3)よりであるから，

　　　　　　　　　　（i.e. ｚはを表す）

(4)より

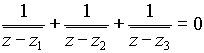
よって

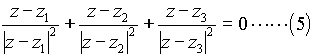
ここで　　

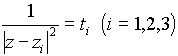　　とおくと

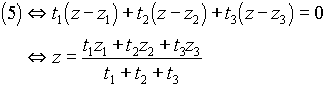
再び

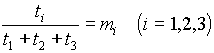　　　とおくとこれはまさに(1)である．

後になって，Ahlforsの「Complex　Analysis」で見るとこのTh．はLucas’s　Theoremで知られるものであった．

Th. If all zeros of a polynomial P(z) lie in a half plane, then all zeros of the derivative P'(z) lie in the same half plane.

さらにここまで書いた後，同僚のＴ先生がこの問題の　はで作られる三角形に内接する面積最大内接楕円の焦点になっている．これは　van den BergのTh．と呼ばれていると教えてくれました．山下純一著の「数学への旅」や、シェーンベルク著の「数学点描」における関連部分を見せてもらいました．　

Back to home